The open Master Hearing Aid Forum

I have received this question by email and have gotten permission to post and answer it here:

For the level tracking in the openmha dynamic compressor dc, were you following the classical definition of time constant, i.e., rise and fall time characterized in terms of reaching 63% of the level? I understand that you didn't explicitly follow the ANSI standard for defining attack/release times. Just wondering if you might be able to speak more to how you evaluated the time constants using your unit tests?



(Remark from Tobias: In this graph, the dark green "Input level" line is mostly hidden by the black "level Fast" line)

The dynamic compressor dc can be configured with 3 different time constants for each frequency band. All three time constants are the time constants(*) of first-order low-pass filters that filter the input level of the frequency band for which they are specified:

tau_rmslev - This time constant is only used when the dc plugin processes waveform input signal, not when it processes spectrum (STFT) signal. The rmslevel filter is a low-pass filter that filters the squared magnitude. The purpose of the rmslevel filter is to protect the subsequent attack and decay filters from the zero-crossings present in normal time-domain signal, i.e. to not convert the zero-crossings to minus infinity dB (-∞dB). This protection is not necessary in the spectral domain. It is also not necessary when dc is driven by the plugin "multibandcompressor", therefore the time constant of the rmslevel filter can be set to 0 in "multibandcompressor" configurations.
tau_attack and tau_decay - Attack and decay filter in plugin dc are first-order low-pass filters that filter level values in dB! The "decay filter" and "decay time constant" are often also called the "release filter" and "release time constant", respectively. In the dc plugin, the attack filter is always applied to the input level measured (in time domain) sample by sample (after the rmslevel filter) or (in spectral domain) measured for each STFT block. The decay (or release) filter is only applied when the level is falling, i.e. when the current output of the attack filter is lower than the previous output of the decay filter. Otherwise (when the level rises), the decay filter will not be applied, but passes through the result of the attack filter. In hearing aid applications, the decay filter time constant is usually significantly larger than the attack filter time constant, so that the additional effect of the attack filter time constant has only minor effect, but it is necessary to be aware of this chaining of the attack and decay filters when the decay filter time constant reaches similar durations as the attack filter time constant.

Now to your question: Which meaning of a 'time constant' for a first-order low-pass filter do we use in the openMHA dc plugin?

We use this definition of the step response: Assume that the filter is completely adapted to input level L1. This means, the filter has seen the input level L1 for the past infinity seconds. Now, the input level abruptly changes to the different input level L2. How fast does the output level of the first-order low-pass level filter change?

Here, we use the common definition that, after one time constant, the difference between output level (in dB) and input level (in dB) of the filter has been reduced by a factor 1/e (where e is the Euler constant 2.71828...). 1/e is approximately 0.3679, which is the complementary of your 63%. Since you define your 63% as "reaching of the [input] level", I believe that we use exactly your expected definition of time constant in the openMHA dc plugin.

I will update this thread on this weekend with a graph where I try to reproduce your graph with the MHA dc plugin. I am especially interested in how the time constant of attack and decay times combine in the case of falling levels. I will publish my dc configuration so that every openMHA user can reproduce the results.

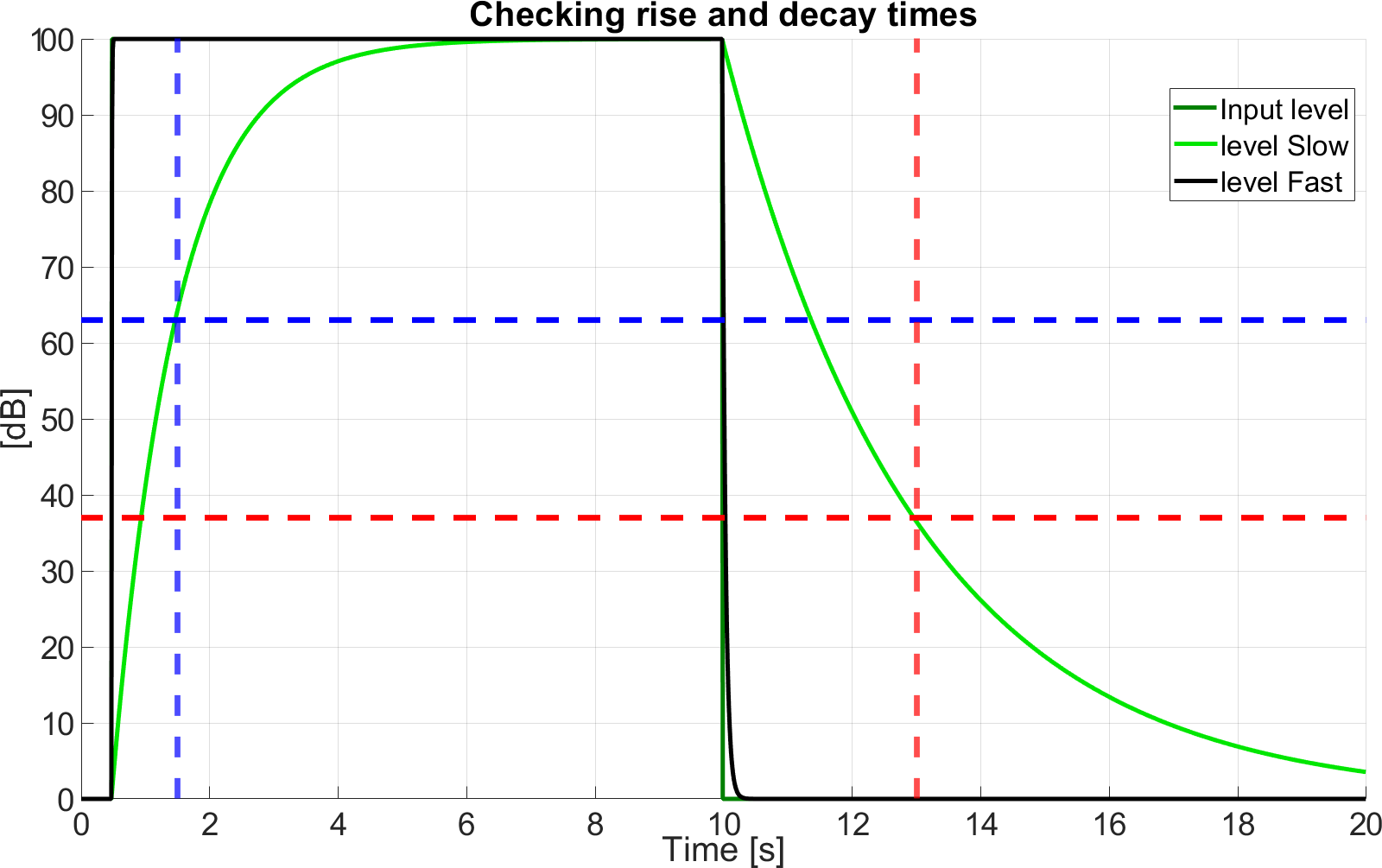
Reproducing your attack time.

Analyzing your graph: You have probably used an attack time constant of exactly 1 second to produce this graph (see analysis at bottom of this post).

This is a very long attack time constant and not suitable for normal hearing aids, but openMHA is very flexible and can simulate an attack time of 1 second in its dc compressor, e.g. using the following configuration: The compressor configured above has only a single band, and does not compress at all for simplicity, because we are only interested in the effect of the attack time constant on the measured input level.
The input signal of the compressor is generated artificially in the MHA configuration itself by the sinusoid generator placed before the STFT overlapadd operation. This way, we do not have to worry about calibration and computing exact input samples to simulate your step response.

The first thing that we want to do is to start the MHA with this configuration and process a signal of level 0dB long enough so that the attack filter of the dc plugin has completely adapted to this input level. Remember that an input level of 0dB is not the same as silence. I am using the MHA io library MHAIOParser in this configuration to be able to read the estimated input level of the dc filter exactly after every 32 input samples.

We can shorten the initial adaptation time of the input level filter by altering tau_attack during this initial adaptation: Appending the following lines to the configuration file will set the attack time constant to 0, then process two audio blocks of 32 samples (the zeros here are replaced by the sine plugin before the dc plugin sees the signal), then changing tau_attack back to the desired attack time constant. I need to process more than one audio block of 32 samples here to fill the complete overlapadd-STFT analysis window with the sinusoid, and I want the window to be completely filled with the sinusoid of level 0dB before changing the attack time constant back to the 1.0 seconds whose effect I want to measure. I can see that the filtered input level is not exactly 0dB but 0.00000026dB which is due to numerical floating-point rounding errors. The error is small enough to be neglected. Finally, I change the level of the sinusoid generator to 100dB, which will be in effect starting with the next incoming audio block.

After the MHA has been initialized with the extended configuration file (mha "?read":tau_attack_test.cfg), I want to process audio blocks and read the filtered level after each block for 1 second of audio signal. 1 second at 48kHz sampling rate means 48000 samples or 1500 blocks of 32 samples each. After that, I expect the filtered input level of the compressor to read 63.21dB.

Therefore, after MHA has been started as above, I need to send it 1500 commands io.input=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0], interleaved with 1500 commands mha.overlapadd.dc.level_in_filtered?val. On a unix system with netcat installed, I can do this by entering in another terminal the following command: (Users of other systems can e.g. write a suitable loop in Matlab or Octave, or install a unix shell and netcat.) Because I enter a newline inside a double-quoted string, my shell will print a continuation prompt before the second line which I have not included here. The grep command removes the (MHA:success) lines from the output and tr command removes the square brackets from the output vector of filtered levels.

The last filtered level printed and stored to file filtered_levels.txt is 63.21 dB as expected. Plotting the filtered levels with gnuplot: shows the same slow level rising as in your graph.

Appendix: Analysis of your graph (see first post in this thread)
1) Horizontal scale: t=20s is at pixel column \(x_{20}=1581\), t=0s is at pixel column \(x_0=94\), therefore your horizontal scale is \(s_x=\frac{x_{20}-x_0}{20}=74.35\frac{pixel}{second}\). ((1581-94)/20).
2) Your first level change is at \(x=129, t_{up}=\frac{x-x_0}{s_x}=0.47s\).
3) At this time the difference between input level (100dB) and filtered input level (0dB) is 100dB. This difference is reduced by a factor \(1/e=0.3679\), i.e. when the filtered level reaches \((100-36.79)dB = 63.21dB\)
4) Vertical scale: L=0dB is at pixel row \(y_0=-924\), L=100dB is at pixel row \(y_{100}=-45\), therefore your vertical scale is \( s_y=\frac{y_{100}-y_0}{100}=8.79\frac{pixel}{dB}\)
5) The 63.21dB filtered level is therefore reached when the filtered level line crosses pixel row \(y_{63.21}=63.21dB \cdot s_y + L0 = -368.4\). This is the case at pixel column 203, which corresponds to time \(t_{up}+tau_{attack}=\frac{203-x_0}{s_x}=1.47s\), therefore \(tau_{attack}=1.0s\).

A quick addition how we test the time constants in unit tests:

We use a very similar setup to what I did in my previous post: set all filter time constants to 0 except for the one that I want to test, then simulate a step response. But instead of directly querying the filtered output levels, I allowed the compressor to actually compress and then I verified that the level change caused by the compressor can be explained by the gain table lookup using the assumed filtered level.

Checking Release Times

(I use the words "decay" and "release" interchangeably in this thread.)

Classic dynamic compressors in hearing aids often use a significantly longer release (or decay) time constant than attack time constant. The purpose of both time constants is to stabilize gain applied to the input signal, because too quick gain changes can reduce speech intelligibility (by reducing modulation) and can also introduce signal distortion. However, by not following quickly rising input levels (e.g. slamming doors) quickly enough, the resulting overshoots can reach uncomfortable output levels. In order to achieve both, a reasonable protection from overshoots, and a sufficiently stable input level estimation, hearing aid dynamic compressors often use a combination of a short attack time and a longer release time constant.

The openMHA dynamic compressor dc takes this concept a bit further and filters all input levels through the attack filter, regardless if the level currently rises or falls, and only then and only for falling levels filters the result of the attack filter with the decay filter. It is therefore not possible to have a shorter effective time constant for falling levels than for rising levels, but it is possible to have longer effective time constants for falling levels than for rising levels. Still, if the release time constant is significantly longer than the attack time constant, then the dc response will still be dominated by the tau_decay time constants for falling levels and by the tau_attack time constant for rising levels, because of the insignificance of the attack time when compared with the release time.

Using a similar MHA configuration as when reproducing the attack response, I can check the filtered level for falling level steps very similarly as for rising level steps. What's more (this may be specific to the MHA dc compressor as explained in the previous paragraph), I can create the same filter response for falling levels using either the attack filter time constant or the release time constant and setting the other time constant to zero.

In this post I want to investigate what the effective time constant for falling step responses is if attack and release filter have time constants of similar magnitude, e.g. exactly the same duration. For this investigation I will choose both time constants to be (unrealistically) 1 second each.

I will use this MHA configuration to conduct the test: Starting this MHA configuration and then processing blocks of audio while monitoring the filtered level similarly as in the 2nd post in this thread, albeit for a longer duration, I can detect that the difference between input level and filtered input level has fallen to 1/e of the of the original difference after 2.15 seconds, a bit longer than the combination of both time constants. It is also apparent that the response of both filters combined is no longer equal to an ideal exponential function. Given that the sum of both time constants is a good guess for the effective time constant for falling levels when both time constants are equal, and also a good approximation for when one time constant is significantly larger than the other, I would now assume that the effective time constant for falling levels can always be approximated as the sum of tau_attack and tau_decay in the openMHA dc plugin.

Thanks for the detailed explanation Tobias. With the spectrum (STFT) level detection, how do you convert between the dB SPL values of gtmin to gtmax of the gaintable to their relative digital dB RMS values? Since the spectrum level detectors are working on dB intensity values, I assume you have some lines of code which specify how the peak level thats specified in the config file is used to calibrate to the dB RMS intensity values that the level detectors are working with. Where are those lines in the code? Perhaps this is how you are using those pascal values?

But even looking into the methods of MHASignal, there are "(no SPL reference)" comments. I don't see where SPL is related to the digital RMS values which are subsequently squared. Where in the code is the peak level related to the digital RMS values?

Computation of level from signal in openMHA does not need to know the peaklevel that you configured in plugin transducers.

To understand how the level computation from STFT spectra works in openMHA, you need to be aware of two openMHA properties:

1) Central calibration. Because hearing aid signal processing depends on input level, many algorithms for hearing aids need to be able to determine the exact physical input level of the signal that they process. Instead of configuring each algorithm with their own idea of the scaling of the audio signal, level-dependent plugins can rely on our "Central Calibration" feature: The amplitudes of time-domain audio samples are scaled so that their physical unit is the SI unit for pressure, Pascal. See section 1.2.4 of the openMHA application manual. Of course, this does not magically just happen to be that way when you have MHA read audio samples from a sound card. It is the responsibility of the openMHA user to scale the signal correctly so that all level-dependent openMHA algorithms can rely on this convention. A tool that we give our users to achieve this is the plugin "transducers", where you can set the input and output peaklevels, i.e. the physical sound pressure levels that correspond to rectangular waveforms which contain only the (positive and negative) extreme amplitudes allowed by the respective A/D and D/A converters.

2) Scaling of openMHA STFT spectra. This builds on 1). We have two plugins that convert time domain signal to spectral signal, and both provide the same scaling convention for STFT: wave2spec and overlapadd. Please have a look at either plugin in the plugin documentation manual, the paragraphs starting with "The plugin performs the following scaling of the signal" explains the (pragmatic) scaling applied to the spectra. The purpose of this scaling is that not every plugin wanting to compute levels from spectra needs to take into account the analysis window shape, its length, and the zero-padding details.

If you have specific questions to any of these points, I will be happy to help.

One more question of clarification regarding lines 305 to 318 in dc.cpp:
Is it an accurate interpretation that both the low pass filters and the interp function expect values in dB SPL?

Yes the conversion to dB is done by MHASignal::pa22dbspl. See its documentation here: http://mha.hoertech.de/doc/master/names ... bda1c6d1de

mha_real_t MHASignal::pa22dbspl ( mha_real_t x, mha_real_t eps = 0.0f ) inline

Conversion from squared Pascal scale to dB SPL.

Parameters
x squared pascal input
eps minimum squared-pascal value (if x < eps –> convert eps instead), eps < 0 not allowed